Uma coisa interessante acontece quando sobrepomos polígonos regulares com um vértice em comum: um ritmo acontece, de medidas surpreendentes cujo padrão ainda não pude estabelecer.
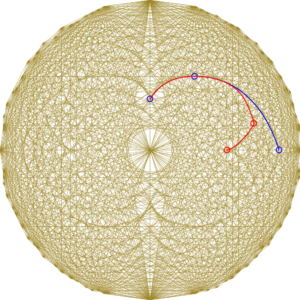
Este é um exemplo composto de polígonos regulares com 3 a 20 lados, unidos por um vértice e com todas as suas diagonais (clique na imagem para abrí-la em seu tamanho original). Dá para perceber o ritmo feito pelas curvas formadas pelas interseções das diagonais (hipociclóides, cáusticas, nefróides), não somente as curvas laterais, mas igualmente as menos perceptíveis, formando arcos côncavos nas linhas horizontais.
Foi procurada uma sequência relacionada a esse ritmo, mas no site The On-Line Encyclopedia of Integer Sequences® (OEIS®), esta não foi encontrada
Na página https://www.chryzode.org/english/cognitif.htm existe uma imagem semelhante a esta, com considerações a respeito dos Crísodos, desenvolvidos pela equipe do site, mas nada sobre as relações entre as curvas internas.
Algumas linhas de construção básicas puderam ser delimitadas dentro do complexo de cruzamentos de diagonais: linhas de arestas de início de curvas na horizontas (cáusticas?, nefróides?) e arestas de curvas às quais dei o nome de “abas laterais” (cáusticas?, nefróides?), na falta de terminologia mais adequada.
Na imagem abaixo, as cúspides cas curvas geradas pela superposição são mostradas, bem como as relações de tamanhos em representações de retângulos, barras e ondas.
Note que os vértices apontados pelas linhas azuis são bem definidos, salvo o que se encontra entre o primeiro e o segundo, de baixo para cima. Clique nas imagens para abrí-las no tamanho original.
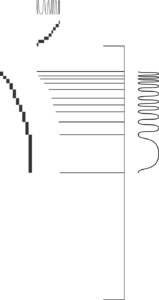
O desenho dos polígonos de 3 a 20 lados, com um dos lados alinhado a uma linha-guia não mostra coisa alguma de relevante ou esteticamente chamativo.
O desenho dos polígonos de 4 a 22 lados, somente de números pares de lados, com um vértice em comum, evidenciou duas curvas com espelhamentos vertical e horizontal, que resultaram em composições de conformação oblonga. Abaixo, as curvas com seus pontos de formação (nodos) vetoriais. Clique nas imagens para abrí-las no tamanho original.
ADENDO
1. Encontrar o número de diagonais de um polígono regular:
K = n(n-3)/2 {n ∈ R | n ≥ 4}
2. Encontrar o número de lados de um polígono regular a partir das diagonais dadas – bastando tirar as raízes na equação de 2º grau, excluindo as raízes negativas:
n(n-3)/2 ⇒ n²-3n-2=0
3. Considere a figura plana obtida pelo desenho de todas as diagonais de um polígono regular de n vértices. Se cada ponto de interseção é associado a um nodo e as diagonais são partidas em cada interseção para formar segmentos associados a vértices, a figura resultante é um gráfico planar, denominado Rn.
Para n = 1, 2, 3, …, a contagem de vértices Vn de Rn é dada pela sequência 1, 2, 3, 5, 10, 19, 42, 57, 135, 171, … (OEIS A007569)