Os algoritmos aplicáveis ao projeto ANACOM são inúmeros. Aqui mostramos alguns e como utilizá-los em Macros ou rotinas de diversas linguagens de programação. Inicialmente, os algoritmos foram divididos em duas classes principais: Caminhos e Algoritmos propriamente ditos. Os Caminhos são as trilhas pelas quais os elementos irão sendo dispostos sobre um gráfico cartesiano pré-definido.
Por exemplo, vamos tomar um gráfico de dimensões 10×10, ou seja, o valor máximo de X é 10 e o de Y é 10. Depois disso, estabelece-se uma sequência baseada na sequência padrão, ou usa-se ela mesma:

Aqui usamos os elementos (a,b,c,d,e,f,g,h,i,j,k,l,m,n), a sequência padrão. Pode-se usar qualquer tipo de sequência para o desenho, por exemplo (a,c,f,i,k,m,b,a,e,e), (a,b,c,d), etc.
Definida a sequência, escolhe-se a trilha a ser seguida. O algoritmo em JavaScript ou outra linguagem irá obedecer, primariamente, à rotação e espelhamento de matrizes. O conjunto de trilhas estabelecidas até agora são as seguintes:
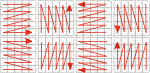 | LINEAR L1 | L2 | L3 | L4 L5 | L6 | L7 | L8 Matriz L1 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | 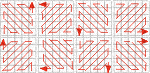 | DIAGONAL D1 | D2 | D3 | D4 D5 | D6 | D7 | D8 Matriz D4 01 02 06 07 15 03 05 08 14 16 04 09 13 17 22 10 12 18 21 23 11 19 20 24 25 | 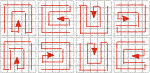 | U U1 | U2 | U3 | U4 U5 | U6 | U7 | U8 Matriz U4 01 02 03 04 05 22 21 20 19 06 23 24 25 18 07 14 15 16 17 08 13 12 11 10 09 |
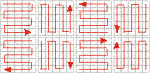 | QUEBRADA Q1 | Q2 | Q3 | Q4 Q5 | Q6 | Q7 | Q8 Matriz Q1 01 02 03 04 05 10 09 08 07 06 11 12 13 14 15 20 19 18 17 16 21 22 23 24 25 | 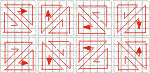 | GREGA G1 | G2 | G3 | G4 G5 | G6 | G7 | G8 Matriz G1 15 16 17 18 19 04 14 24 25 20 05 03 13 23 21 06 01 02 12 22 07 08 09 10 11 | 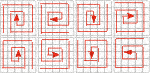 | ESPIRA INTERNA E1 | E2 | E3 | E4 E5 | E6 | E7 | E8 Matriz E4 01 02 03 04 05 16 17 18 19 06 15 24 25 20 07 14 23 22 21 08 13 12 11 10 09 |
MONTAGEM
Suponhamos que se escolha o primeiro caminho da primeira figura dos caminhos (com direção da esquerda para a direita em todas as linhas – vai-e-volta), ou Caminho L1, com a sequência original (A,B,C,D,E,F,G,H,I,J,K,L,M,N). Os elementos então seguirão este caminho, exatamente na sequência escolhida. Tendo esses dados, estabelecemos ainda que a Matriz, ou o desenho resultante, terá 10 letras em cada linha (Largura = 10) e 10 linhas (Altura = 10). O desenho resultante neste caso será:

ABCDEFGHIJ
KLMNABCDEF
GHIJKLMNAB
CDEFGHIJKL
MNABCDEFGH
IJKLMNABCD
EFGHIJKLMN
ABCDEFGHIJ
KLMNABCDEF
GHIJKLMNAB
Como se pode observar, existe um padrão de repetição de início de linhas, a partir da linha 8. Isso que dizer que, para esta sequência em particular, com Largura = 10, basta ter Altura = 7 para se ter um padrão completo.
OUTRO EXEMPLO: Com L=5 e A=5, e a mesma sequência anterior, mas tendo o caminho Q1:
ABCDE
JIHGF
KLMNA
FEDCB
GHIJK
| Fica mais fácil fazer esse tipo de painel usando letras de outra fonte ao invés das imagens da fonte ANACOM.TTF de início, convertendo o desenho depois. Dica: Um dos processos mais interessantes de se fazer um desenho é jogar com elementos que sejam como imagens em negativos umas das outras, como por exemplo A/N, B/D, C/E, F/L, G/M, H/J e I/K. Usando estes pares, consegue-se fazer um desenho repleto de ‘trilhas’, o que pode gerar, em desenhos de dimensões grandes (maiores que 200 elementos), efeitos interessantes e surpreendentes. |
EQUAÇÕES
As Equações propriamente ditas funcionam com base nas coordenadas do gráfico cartesiano (cuja origem está no ponto (1,1) e de crescimento positivo para ambos X e Y (ou seja, do canto inferior esquerdo para o canto superior direito). Por exemplo, tome-se a equação x² + y². Ela não é resolvida como uma equação de segundo grau, é simplesmente uma conta feita com os valores de X e Y no gráfico do desenho.
Usando como referência a sequência (B,C,D,E), transpomos os resultados dos cálculos nos pontos do gráfico da seguinte maneira:
Antes de mais nada, devemos considerar que cada posição no gráfico tem uma coordenada X e Y. Imagine um papel quadriculado, onde você delimitou o tamanho final do seu desenho, digamos A=4 e L=6. Agora, faça um esquema para não se perder nas coordenadas. Escreva os números das linhas e colunas neste gráfico, da seguinte maneira:
4| | | | | | |
3| |•| | | | | <- O • está no ponto (2,3), ou seja, x=2 e y=3
2| | | | | | |
1| | | | | | |
_|1|2|3|4|5|6|
Para x = 2 e y = 3, o resultado deste ponto (2,3) será o número (2^2 + 3^2 => 4 + 9) = 13, a aplicação da equação. O número 13 corresponde à letra B. Para facilitar a visualização, mostramos aqui a matriz gerada para os números atribuídos às letras dos elementos e o desenvolvimento do desenho:
B|1 5 9 13 17 | Vamos fazer as contas: 4|17|20|25|32|41|52 | Vamos transformar os números nas letras da sequência: 4|B |E |B |E |B |E |
Virtualmente qualquer equação poderá ser usada nos desenhos; basta transpor os valores de X e Y nas equações, calcular e transformar os resultados nas letras dos elementos. É um método trabalhoso e talvez complicado, mas os resultados são muito interessantes. Veja os exemplo 1 e exemplo 2 para ter uma idéia melhor.
EXEMPLO 1
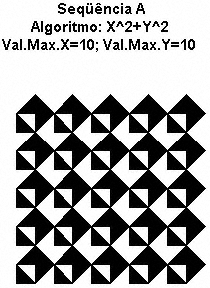
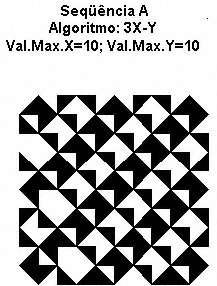
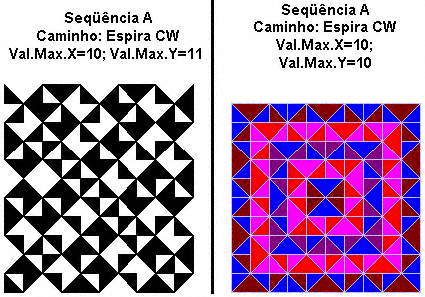
EXEMPLO 2

